题目内容
（请给出正确答案）
[主观题]
证明：设A，B皆为nxn实对称矩阵，且互相交换，则它们有公共的特征向量作为欧氏空间Rn的标准正交基。
答案
查看答案
重要提示：请勿将账号共享给其他人使用，违者账号将被封禁！
查看《购买须知》>>>
请输入或粘贴题目内容
搜题
拍照、语音搜题，请扫码进入小程序
题目内容
（请给出正确答案）
答案
更多“证明：设A，B皆为nxn实对称矩阵，且互相交换，则它们有公共的特征向量作为欧氏空间Rn的标准正交基。”相关的问题
第2题
(1)设A、C分别为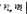
阶实对称矩阵，B是
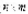实矩阵，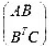
是正定矩阵(实)。证明:
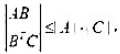等号当且仅当B=0时成立.
(2)设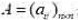
是n阶实矩阵，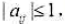
求证:
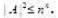
第5题
设A是nxn对称正定矩阵，并设v(i)，i=0，1，...，n-1为线性无关的一组向量。令p(k)，k=0，1，...，n-1，如下生成：
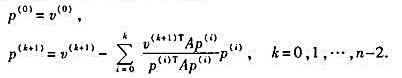
证明：方向p(k)，k=0，1，...，n-1，是A共轭的。上述过程称为共轭化，它从一组线性无关方向出发，产生一组A共轭方向。
第7题
设A是实对称矩阵，且A2=0，证明A∞0。
(提示：注意A的对角线上的元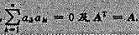
)
